2022-2023衡水金卷先享题 高三一轮复习周测卷(老高考)/语文(四)4答案

2022-2023衡水金卷先享题 高三一轮复习周测卷(老高考)/语文(四)4答案，目前全国100所名校答案网已经汇总了2022-2023衡水金卷先享题 高三一轮复习周测卷(老高考)/语文(四)4答案的各科答案和试卷，更多全国100所名校答案请关注本网站。

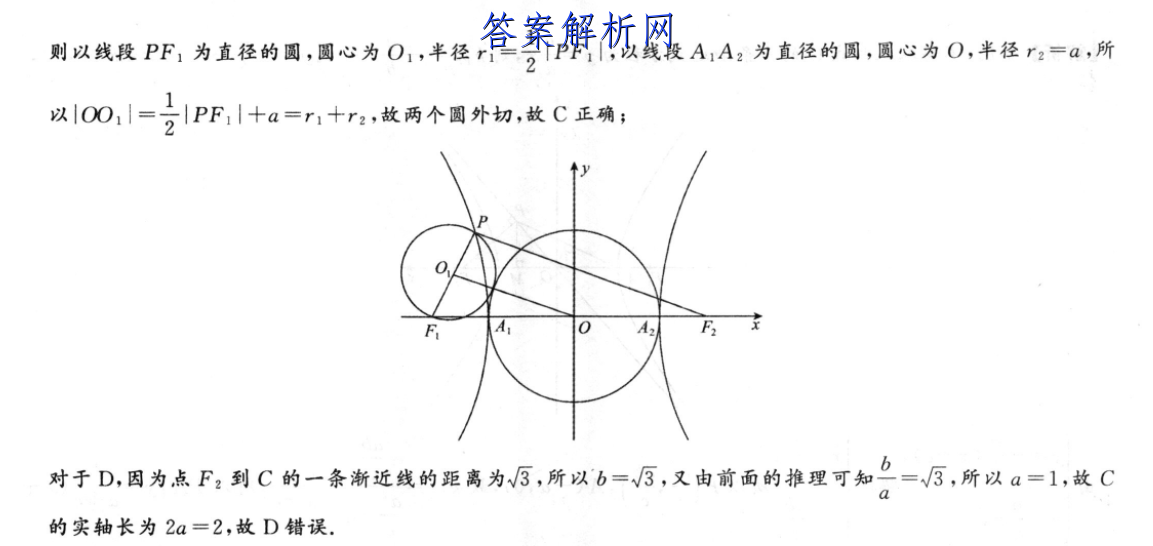
22y21.已知双曲线C:。一方=1(>0，b>0)的左、右焦点分别为F,F:,左、右顶点分别为A1,A:,P为双曲线的左支上一点，且直线PA,与PA2的斜率之积等于3，则下列说法正确的是A.双曲线C的离心率为√3B.若PF1⊥PF2,且S△PF1F2=3,则a=2C.以线段PF1,A1A2为直径的两个圆外切D.若点F2到C的一条渐近线的距离为√3，则C的实轴长为4【答案】C【解析】对于A,设P(xy),则y2=b(-1,图为A1(一a,0),A:(a,0),直线PA,与PA:的斜率之积等于=y2b.b23,所以kA,·kpA,=x十a‘x-a=z=Q=3,得e=√1+0=2，故A错误；对于B,因为e==2,所以0c=2a,而P为双曲线的左支上一点，根据双曲线的定义可得|PF2|一|PF,|=2a,又因为PF1⊥PF2,且SAm,=3,所以Sa55,=2PF,·PF:=3,则PF,1PF,=6,由PF,P+PFP=(2c),可得(PF,|-|PF2|)2+2|PF1|·|PF2|=4c2,即4a2+12=16a2,解得a=1,故B错误；对于C,如图，设PF1的中点为O1,0为原点，则O0为△PF,F,的中位线，所以00l=21PF,=2(PF,+2a)=PF+a,则以线段PF,为直径的国，圆心为O,半径r1=号PF,以线段AA:为直径的圆，周心为O,半径，=a,所以00=号PF,十a=r十r,故两个圆外切，故C正确；FA0A2对于D,因为点F,到C的一条渐近线的距离为5，所以b=5,又由前面的推理可知=3，所以a=1,故C的实轴长为2a=2,故D错误.

14.已知A,B是抛物线y2=4x上的动点，且满足|AB|=10,则AB中点M的横坐标x。的最小值为【答案】4【解析】设抛物线y2=4x的准线为l,焦点为F,则L:x=一1，过点A作AA1⊥1于A1,过点B作BB1⊥1于B1,连接FA,FB,则2(xo+1)=|AA1|+|BB1|=|FA|+|FB|≥|AB|=10,得xo+1≥5，解得xo≥4，所以x。的最小值为4.